Vibrations

In this type of project, the vibrational modes are calculated from a finite difference approximation of the Dynamical matrix.

The project starts with the definition of the atomic structure. We refer the user to section Structure Modeling in ASAP for further information on ASAP structure builder/viewer interface.

After the atomic structure is defined, edit the type of project by selecting Vibrations from the list of possible project types implemented in ASAP.

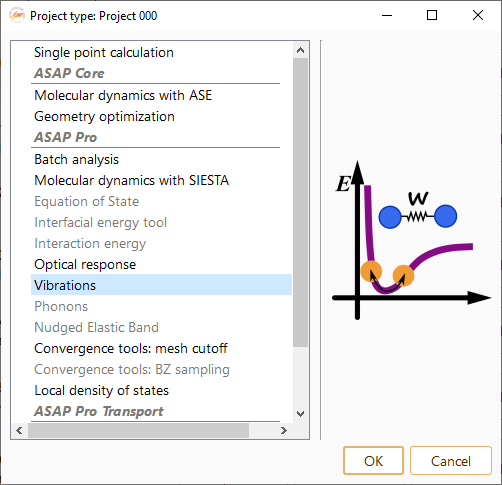
Then click on the Parameters icon to open the Vibration parameters widget.

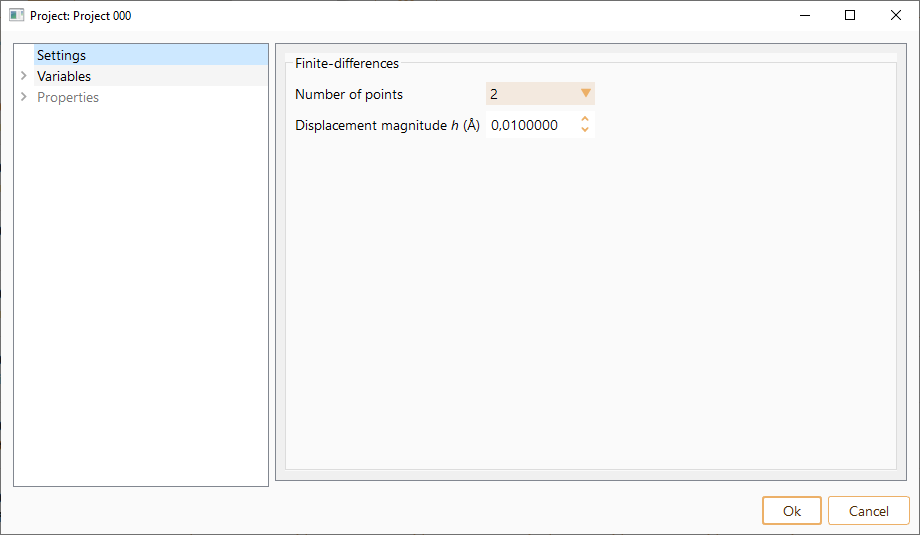
The project parameters that can be tuned are:

• Number of points. Number of displacements per atom and cartesian coordinate. The number of displacements supported are 2 and 4.

  • Number of points 2: Displacement of each atom by the values +\(\Delta\) and -\(\Delta\) for each cartesian coordinate.

  • Number of points 4: Displacement of each atom by the values +\(\Delta\), +two times \(\Delta\), -\(\Delta\), and -two times \(\Delta\) for each cartesian coordinate.

  Notice that the displacement is applied to each atom in the configuration. When performing a vibration project, one may wish to keep some degrees of freedom in the system fixed. We refer the user to section ASE GUI in ASAP for information of setting constraints.

• Displacement magnitude h (Å). Parameter giving the magnitude of displacements. Unit: Å

Click on the Calculator icon to select the computational engine to be used during vibration calculation.

We refer the user to chapter Calculators for further information on ASAP available calculators.

Click on the Run icon to open Run widget. Then press the Run button to submit the vibration calculation.

We refer the user to chapter Runners for further information on computational resources configuration in ASAP.

After submitting a job, the tab Calculator output in Run widget shows the complete calculation output in real time.

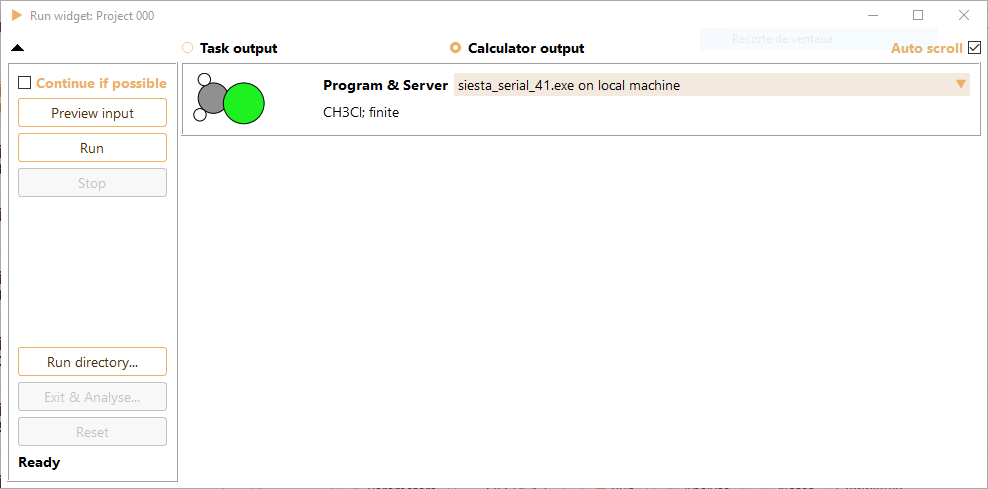
In addition, the tab Task output in Run widget shows relevant information of Vibration output in real-time.

Vibrations workflow: Analysis

When the calculation is completed, select Exit and analyse to open the analysis widget.

After a successful vibration project run, you can analyse the following information:

Density of vibration modes The density of vibrational modes is defined by \(Density(w) = \sum_i \delta(w-E_i)\), where w is frequency at which the density of vibrational modes is computed, the sum runs over vibrational modes i, \(E_i\) is frequency of the vibrational mode i. \(\delta\)(w) is the Dirac \(\delta\)-function.

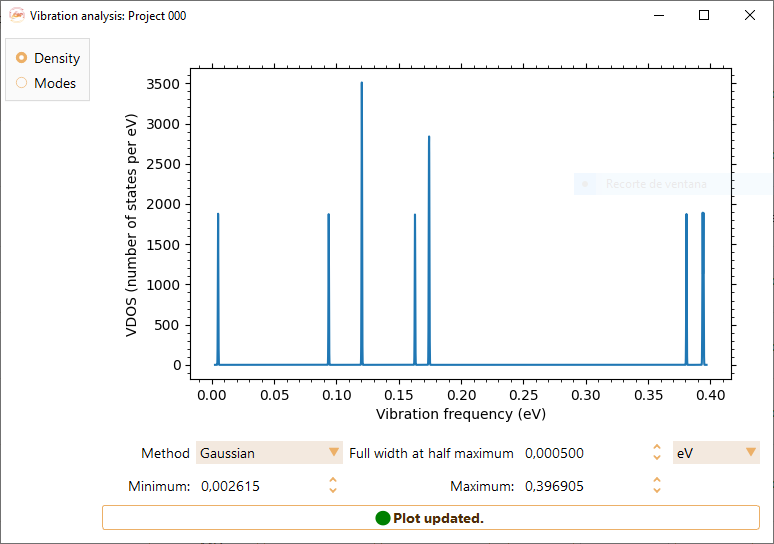
You can adjust the following parameters in the representation of density of vibrational modes:

• Method. Gaussian or Lorentzian representations of the Dirac \(\delta\)-function.

  

• Minimum and Maximum. They are the start and end values of the Gaussian/Lorentzian in units of eV, meV, Ry, Ha, THz, K, and cm^-1.

  

• Width at half maximum. Broadening defined by the full-width-at-half-maximum in both representations (Gaussian and Lorentz) of the \(\delta\)-function.

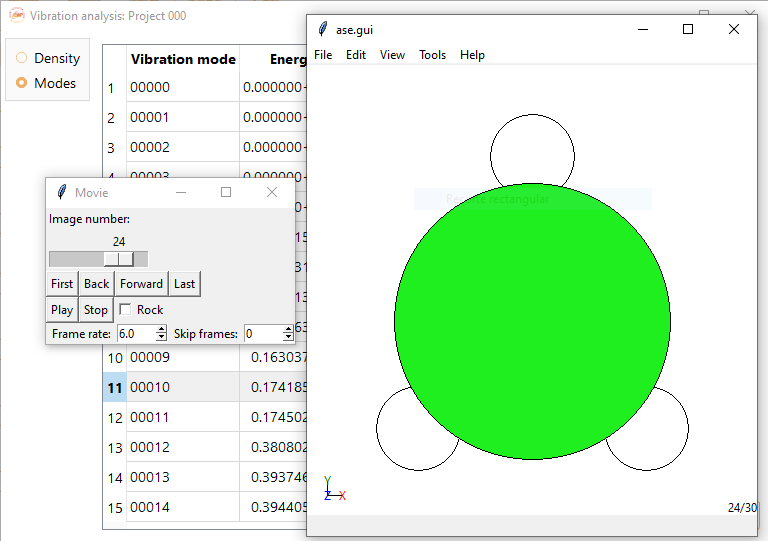
Vibration modes

This analysis option presents the computed vibrational modes list alongside their corresponding energies. Additionally, it offers the zero-point vibrational energy (ZPVE).

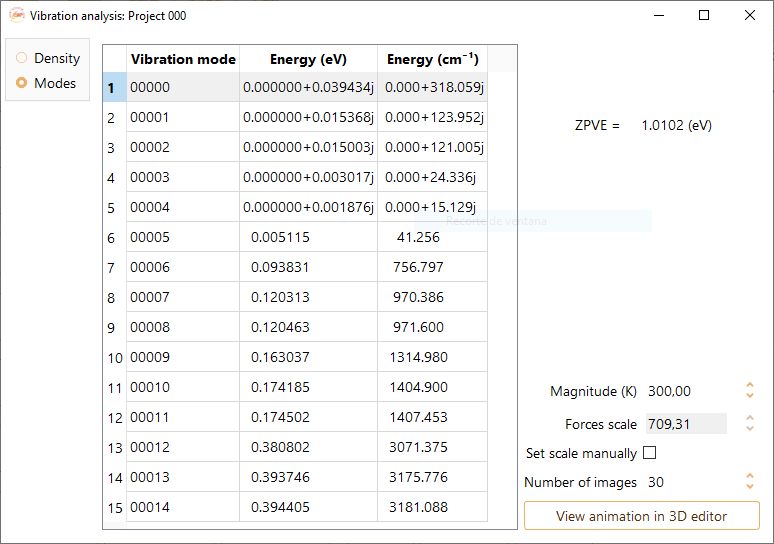
To see an animation of one of the computed vibrational modes, select it first from the list, and then click on the View animation in 3D editor button. The following settings can be tuned before viewing the animation:

• Magnitude: Temperature (in K) associated to the energy (E(\(\nu\))) of the selected vibrational mode.

• Force scale: Parameter only available when Set scale manually tick-box is activated

• Number of images: Number of images that will be included in the animation.

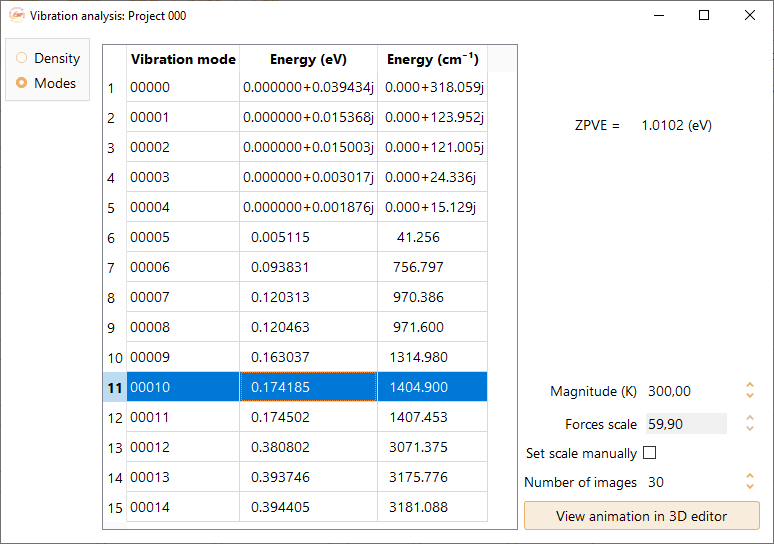
Play the movie to visualise the animation of the selected vibrational mode.

We refer the user to section ASE GUI in ASAP for further information on the features implemented in ASE GUI.