Overview of ASAP Workflows#
We have designed ASAP workflows to help you in all necessary steps involved in a computer simulation,
Preparing the material model.
Defining the properties of interest.
Setting up the input parameters for the simulation.
Running/submitting the calculation.
Analysing results.

Single-point calculation - (SIESTA, Quantum ESPRESSO)
A single-point energy calculation calculates the wave function and charge density, and hence the energy, of the particular arrangement of nuclei defined by the atomistic model (well-specified geometric structure). The computed energy is the total energy (sum of the electronic energy and nuclear repulsion energy).
Molecular Dynamics - (SIESTA, Quantum ESPRESSO)
The Molecular Dynamics (MD) type of project performs dynamics of the system in time. At each time step, ab initio calculations are performed and the forces acting on each atom are extracted. The position of the atoms is updated with respect to these forces using classical equations of motion (Newton’s second law). MD is computing electronic structure, forces and stresses for the system geometry at each time step, updating the atomic positions and proceeding to the next cycle. ASAP includes several algorithms to perform MD calculations.
Geometry Optimisation - (SIESTA, Quantum ESPRESSO)
The determination of equilibrium structure is of fundamental importance in the modelling of materials at the atomic scale. In this type of project, the calculation starts from a well-specified geometric structure. Then, the atoms are moved to try to minimise the forces (and stresses) acting on them. Several methods for the structure geometry optimisation are available. All of them try to locate minima and saddle points on the Potential Energy Surface (PES).
Equation Of State (EOS) - (SIESTA, Quantum ESPRESSO)
The workflow implemented in this type of project automates the computation of energy (E) versus volume (V) curve. The curve is fitted to the selected universal Equations of State (EOS) (Murnaghan’s, third-order isothermal Birch-Murnaghan’s, exponential Vinet’s…) to compute equilibrium properties such as bulk modulus (B).
Nudged Elastic Band (NEB) - (SIESTA)
Nudged Elastic Band (NEB) is a method for finding saddle points (transition state) and minimum energy paths between known reactants (initial state) and products (final state). ASAP facilitates all the steps involved in the workflow of a NEB simulation.
Phonons - (SIESTA)
We have implemented a workflow to automate the computation and analysis of phonons of a periodic system.Our implementation uses the so-called small-displacement or frozen-phonons method as has been done in ASE (https://wiki.fysik.dtu.dk/ase/ase/phonons.html). The non-analytic contributions to the dynamical matrix are currently not treated. On the other hand, we perform the computation of the dynamical matrix in reciprocal space with a Parlinski method (https://doi.org/10.1103/PhysRevLett.78.4063). The Vibra utility, available within the SIESTA package, inspired our implementation. (siesta-project/siesta/-/blob/master/Util/Vibra).Vibrations - (SIESTA)
ASAP automates the calculation of vibrational modes of a well-specified geometric structure. The vibrational frequencies are calculated from a finite difference approximation of the Hessian matrix.
Optical response - (SIESTA)
ASAP automates the calculation of the optical response of a system; real and imaginary part of the dielectric function. The approach used is based on computing the dipolar transition matrix elements between different eigenfunctions of the self-consistent Hamiltonian.
Interaction energy - (SIESTA) The workflow implemented in this type of project automates the computation of the interaction energy of a system built out of two subsystems.
Interfacial energy tool (IET) - (SIESTA)
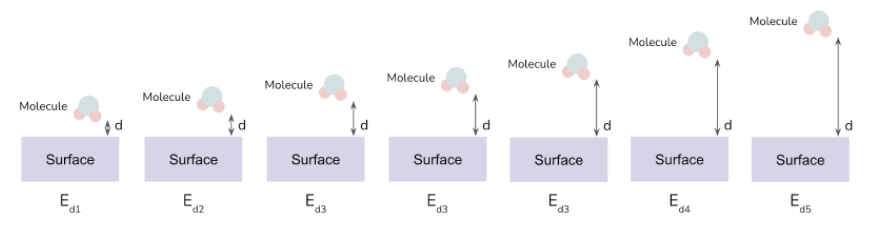
The workflow implemented in this type of project automates the computation of single-point calculations of a system built out of two subsystems placed at different distances (d).
Convergence Tools: mesh cutoff - (SIESTA)
Siesta uses a finite 3D grid for the calculation of some integrals and the representation of charge densities and potentials. Its fineness is determined by its plane-wave cutoff, as given by the MeshCutoff option. It means that all periodic plane waves with kinetic energy lower than this cutoff can be represented in the grid without aliasing. In turn, this implies that if a function (e.g. the density or the effective potential) is an expansion of only these plane waves, it can be Fourier transformed back and forth without any approximation.
Mesh cutoff convergence can be used to diagnose the eggbox effect to be expected for a particular pseudopotential/basis-set combination. The energy as a function of atomic coordinates displacement is computed. The eggbox period is evaluated for the selected Mesh cutoff values.
Convergence Tools: Brillouin Zone sampling - (SIESTA)
In this type of project, ASAP runs a set of single-point calculations using the selected Brillouin zone (BZ) sampling grids. ASAP uses Monkhorst-Pack grids to sample the Brillouin zone. A Monkhorst-Pack grid is a set of evenly spaced k-points and is specified by 3 numbers: the number of points along each axis in reciprocal space.
Local density of states (LDOS) - (SIESTA)
The Local density of states (LDOS) type of project describes the density of states, which is essentally the number of different states at a particular energy level that electrons are allowed to occupy, but space-resolved.
Transport - (SIESTA)
This type of project allows to solve the electronic structure of an open system formed by a finite structure sandwiched between two semi-infinite metallic leads. A finite bias can be applied between both leads, to drive a finite current.
